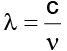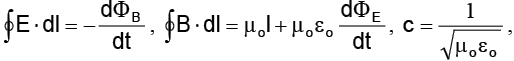dr n. med. Andrzej Styszyński
okulista, starszy wykładowca Laboratorium Fizyki Widzenia i Optometrii Wydziału Fizyki Uniwersytetu im. Adama Mickiewicza w Poznaniu,
ekspert Krajowej Rzemieślniczej Izby Optycznej
Chociaż elektrodynamika kwantowa potrafi wyjaśnić wszystkie obserwowane zjawiska świetlne, to niektóre z nich, takie jak dyfrakcja, interferencja i polaryzacja, mogą być całkowicie, a przy tym łatwiej wytłumaczone przez klasyczną teorię falową. Dlatego też, aby zrozumieć istotę polaryzacji światła, będziemy posługiwać się właśnie jego teorią falową.
Przyjmujemy, że światło widzialne to fala elektromagnetyczna o długości
λ 
(380,740) nm.
Temu przedziałowi długości fali odpowiada częstotliwość
ν 
(4,1; 7,9)·1014 Hz, ponieważ:
,
gdzie:
– długość fali,
– częstotliwość,
c = 3·108 m/s – prędkość światła w próżni.
Równania Maxwella
Istnienie fal elektromagnetycznych przewidział brytyjski fizyk James Clerk Maxwell. Wiedziony genialną intuicją naukową, przedstawił swoje przeczucia w 1865 r. w postaci równań, które na jego cześć zostały nazwane równaniami (lub prawami) Maxwella.
Osobiście uważam je za bardzo piękne i myślę, że można je nazwać czystą poezją zapisu matematycznego praw fizycznych opisujących powstawanie fal elektromagnetycznych. Z tego powodu nie potrafię oprzeć się pokusie, by przypomnieć je naszym czytelnikom.
gdzie:
E – natężenie pola elektrycznego,
B – indukcja pola magnetycznego,
ΦB – strumień indukcji pola magnetycznego,
ΦE – strumień natężenia pola elektrycznego,
I – natężenie prądu elektrycznego,
t – czas,
μo – przenikalność magnetyczna próżni,
εo – przenikalność elektryczna próżni,
c – prędkość światła w próżni.
Nie wdając się w dokładne wyjaśnianie szczegółów powyższych równań, ograniczę się jedynie do podania ich sensu fizycznego:
- zmienne pole magnetyczne wytwarza wirowe pole elektryczne, a cyrkulacja wektora natężenia pola elektrycznego E jest równa szybkości zmian strumienia wektora indukcji (natężenia) B pola magnetycznego;
- zmienne pole elektryczne wytwarza wirowe pole magnetyczne, a cyrkulacja wektora indukcji B pola magnetycznego jest równa szybkości zmian strumienia wektora natężenia E
pola elektrycznego; - wirowe pole magnetyczne może być także wytworzone
wokół przewodnika z prądem o natężeniu I.
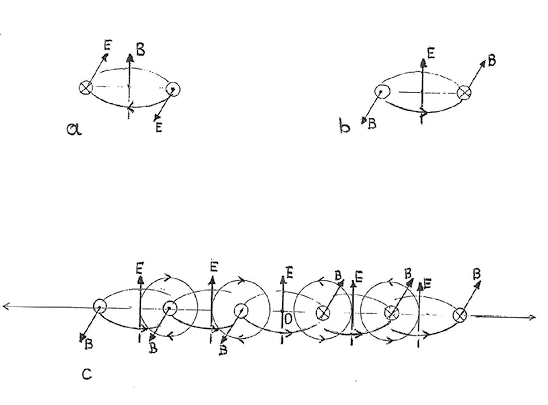
Ryc. 1. Schemat powstawania fali elektromagnetycznej.
Zmiana indukcji B pola magnetycznego powoduje tworzenie
wirowego pola elektrycznego o natężeniu E (a).
Zmiana natężenia E pola elektrycznego jest przyczyną powstawania
wirowego pola magnetycznego B (b).
Zmiany natężenia pola elektrycznego E, zachodzące w punkcie O, wywołują falę elektromagnetyczną rozchodzącą się w próżni w kierunku x (c).
Jeżeli w próżni wytworzymy zmienne pole magnetyczne,
to wywoła ona wirowe pole elektryczne. To nowe (też zmienne) pole elektryczne wytworzy następne nowe zmienne pole magnetyczne, a to z kolei nowe pole elektryczne i tak dalej…
Wystarczy więc wytworzyć w jakimś miejscu przestrzeni zmienne pole elektryczne lub magnetyczne, aby uruchomić ten łańcuch przyczynowo-skutkowy, czyli falę elektromagnetyczną, która mknie w przestrzeni z prędkością światła
Te piękne prawa – w momencie ich pierwotnego przedstawienia jeszcze tylko teoretyczne – zyskały doświadczalne potwierdzenie dzięki Heinrichowi Herzowi, który w roku 1886 wytworzył falę elektromagnetyczną, posługując się skonstruowanym przez siebie oscylatorem.
Wektory natężenia pola elektrycznego E i indukcji pola magnetycznego B fali elektromagnetycznej są prostopadłe względem siebie i względem wektora prędkości rozchodzenia się fali. Fala elektromagnetyczna (czyli także fala świetlna) jest falą poprzeczną.
Falom radiowym, których źródłem są drgania ładunku elektrycznego w antenie (zachodzące w jednym kierunku), odpowiadają drgania wektora natężenia pola elektrycznego, które zachodzą w jednej płaszczyźnie, zwanej płaszczyzną drgań. Fale o takim charakterze nazywamy falami liniowo spolaryzowanymi.
Dla uproszczenia, ryciny 1 i 2 przedstawiają jedynie linie natężenia pola elektrycznego (leżące w płaszczyźnie rysunku) i linie indukcji pola magnetycznego (w płaszczyźnie prostopadłej do rysunku). Stan taki odpowiada właśnie fali elektromagnetycznej
spolaryzowanej liniowo.
Warto zauważyć, że naturalne źródła światła widzialnego wysyłają światło niespolaryzowane. Dzieje się tak dlatego, że źródła te składają się z olbrzymiej liczby emiterów, czyli atomów i cząsteczek emitujących fale świetlne w najrozmaitszych kierunkach przestrzeni. W ten sposób wiązka światła niespolaryzowanego jest zespołem fal, w których drgania wektorów natężenia pola elektrycznego (i oczywiście magnetycznego) odbywają się w bardzo wielu płaszczyznach.
Ponieważ w fali świetlnej pole magnetyczne jest zawsze prostopadłe i proporcjonalne do pola elektrycznego, w rozważaniach stanu polaryzacji światła rozpatrywać będziemy – dla uproszczenia – jedynie pole elektryczne.
Ryc. 3. Pole elektryczne E dla światła niespolaryzowanego (a) i spolaryzowanego liniowo (b), biegnącego prostopadle do płaszczyzny ryciny.
Ogólnie rzecz biorąc, ludzkie oko nie jest wrażliwe na polaryzację światła. Wyjątkiem w tym względzie jest zjawisko „śmigła” Haidingera. W przyrodzie występują jednak organizmy, które reagują na kierunek polaryzacji światła. Należą do nich pewne owady, m.in. pszczoły.
Warto dodać, że ludzkie oczy, a także oczy zwierząt i owadów, reagują na składową elektryczną światła. Składowa magnetyczna nie działa na siatkówkę oka.
Otrzymywanie światła spolaryzowanego
Do polaryzacji światła służą specjalne przybory zwane
powszechnie polaryzatorami.
Polaryzację światła można przeprowadzić w różny sposób, m.in.:
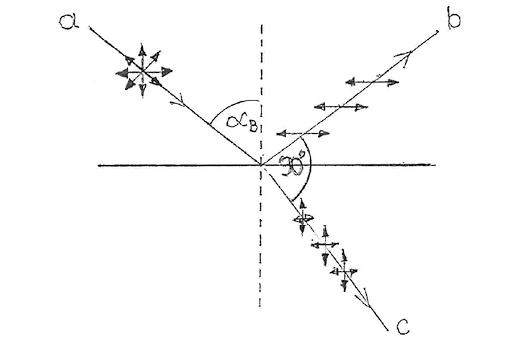
- przez odbicie wiązki światła od szkła (lub innego dielektryka) pod odpowiednim kątem αB, zwanym kątem Brewstera, którego wartość spełnia warunek: tgαB = n, gdzie n oznacza współczynnik załamania (indeks) szkła.
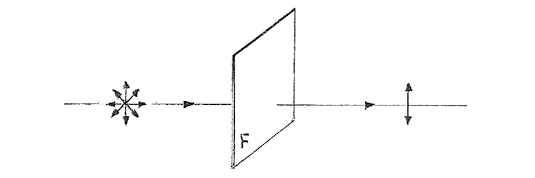
Ryc. 4. Odbicie światła pod kątem Brewstera αB: a – niespolaryzowany promień padający, b – spolaryzowany liniowo promień odbity, c – częściowo spolaryzowany promień załamany. - przez wykorzystanie tzw. kryształów dwójłomnych (np. kalcyt, rutyl), które rozszczepiają wiązkę śwwiatła niespolaryzowanego na dwie wiązki światła spolaryzowanego liniowo.
- przez zastosowanie filtrów polaryzacyjnych, które są utworzone przez długie łańcuchy organicznych molekuł i przepuszczają światło o określonym kierunku drgań pola elektrycznego.
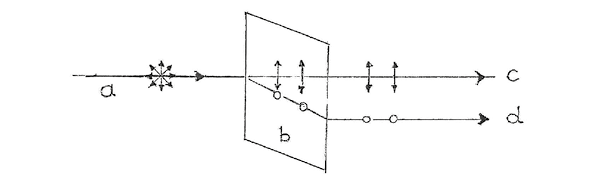Ryc. 5. Wiązka światła niespolaryzowanego (a), przechodząc przez kryształ dwójłomny (b), ulega rozszczepieniu na promień zwyczajny (c) i nadzwyczajny (d), które są liniowo spolaryzowane w płaszczyznach do siebie prostopadłych.
Właśnie tego rodzaju filtry polaryzacyjne (np. błony jodkowo-poliwinylowe, siarczan jodochininy) są obecnie najczęściej stosowane w optyce okularowej, okulistyce i optometrii.
- z wykorzystaniem wyświetlaczy ciekłokrystalicznych LCD
(ang. liquid-crystal displays). Są to urządzenia wyświetlające obraz, których zasada działania oparta jest na zmianie polaryzacji światła na skutek zmian orientacji cząsteczek ciekłego kryształu pod wpływem przyłożonego pola elektrycznego. Monitory ekranowe służące do prezentacji optotypów i różnych testów do badania widzenia obuocznego to monitory ciekłokrystaliczne.
Układy dwóch filtrów polaryzacyjnych
W diagnostyce okulistycznej i optometrycznej często wykorzystuje się – zwłaszcza w badaniu widzenia obuocznego – układ dwóch filtrów polaryzacyjnych (ryc. 7).
Ryc. 7. Przejście światła przez układ dwóch polaryzatorów: P1 – polaryzator pierwszy, P2 – polaryzator drugi, α – kąt pomiędzy płaszczyznami polaryzacji obu polaryzatorów.
Jeżeli natężenie wiązki światła po przejściu przez pierwszy polaryzator P1 wynosi I1, to po przejściu przez drugi polaryzator
P2 (niekiedy nazywany analizatorem) wynosi
I2 = I1 cos2α,
gdzie α – kąt pomiędzy płaszczyznami polaryzacji obu
polaryzatorów.
Jeśli więc płaszczyzny polaryzacji obu polaryzatorów są równoległe, czyli α = 0o, to cos0o = 1 i drugi polaryzator przepuszcza światło spolaryzowane w tej samej płaszczyźnie.
Jeżeli natomiast płaszczyzny polaryzacji obu polaryzatorów są prostopadłe, czyli α = 90o, to cos90o = 0 i drugi polaryzator
światła nie przepuszcza.
Takie układy dwóch filtrów polaryzacyjnych są wykorzystywane w testach służących do badania refrakcji oraz widzenia obuocznego. Jak pamiętamy, badanie refrakcji zwykle kończymy zrównoważeniem bodźca do akomodacji. To zrównoważenie bodźca do akomodacji (zwane także balansem obuocznym) można przeprowadzić na kilka sposobów. Jeden z nich, właśnie z wykorzystaniem światła spolaryzowanego, przedstawia rycina 8.
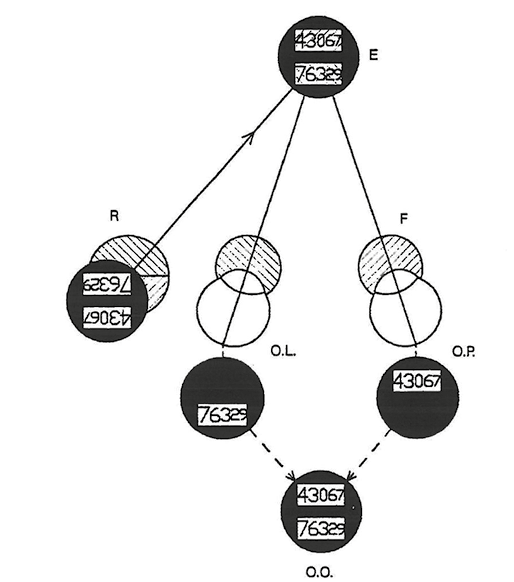
Ryc. 8. Test polaryzacyjny do budowania równowagi refrakcji (czarne optotypy na jasnym, oświetlonym spolaryzowanym światłem tle): R – rzutnik, E – ekran, F – filtr polaryzacyjny, O.P. – oko prawe, O.L. – oko lewe, O.O. – wrażenie obuoczne (równowaga refrakcji).
Przykładem wykorzystania filtrów polaryzujących w optyce okularowej są (dobrze znane optykom, bo od wielu lat przez nich stosowane) polaryzujące okulary słoneczne. Okulary takie są szczególnie użyteczne w redukowaniu olśnienia spowodowanego odbitym światłem słonecznym. Jak już wiemy, światło odbite od powierzchni wody jest w pewnym stopniu (a dla kąta Brewstera – całkowicie) spolaryzowane równolegle do tej powierzchni, a więc poziomo.
Z tego powodu okulary słoneczne, aby blokować poziomo spolaryzowaną składową światła odbitego, mają pionowo ustawioną płaszczyznę filtrów polaryzacyjnych. Przydatność takich okularów jest oczywista, zwłaszcza w żeglarstwie i dla kierowców chcących uniknąć olśnienia światłem odbitym, np. od mokrego po deszczu asfaltu.
Czytelnicy pamiętają zapewne, że współczynnik załamania wody n = 1,33, a więc przy odbiciu światła od powierzchni wody
tgαB = 1,33, stąd αB = 53o. Gdy słońce znajduje się na wysokości 37o nad horyzontem, promienie słoneczne odbite od powierzchni wody są całkowicie spolaryzowane.
Najczęściej stosowane do badania widzenia obuocznego polaryzacyjne testy Haasego przedstawimy w następnym numerze „Optyka Polskiego”.
